曲線について

・	曲線を引くためには
・	２次ベジェ曲線を描画する
・	３次ベジェ曲線を描画する
・	Ｎ次ベジェ曲線を描画する
・	スプライン曲線を描画する

前のページに戻る

曲線を引くためには

■曲線上の座標を得る

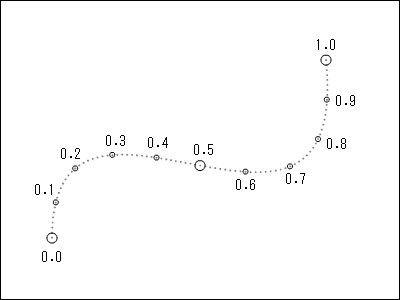
曲線の開始を 0.0 、曲線の終了を 1.0 として、

0.0 ～ 1.0 までの数値を指定すると、該当する座標を取得する事ができます。

これがこれから紹介する曲線上の座標の基本的な取得方法となります。

■曲線を描画するには

等間隔で曲線上の座標を、何個か取得します。

例えば、

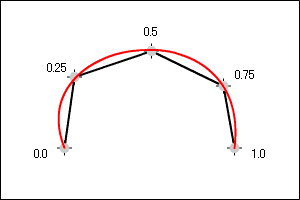
「0.0、0.25、0.5、0.75、1.0」という 5 個の座標を取得したとします。

この 5 個の各座標を、直線で描画して繋ぐと以下のようになります。

次は、

「0.0、0.1、0.2、0.3、0.4、0.5、0.6、0.7、0.8、0.9、1.0」という 11 個の座標を取得したとします。

この 5 個の各座標を、直線で描画して繋ぐと以下のようになります。

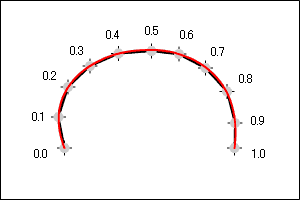
以上の事から、

綺麗な曲線を描画するには、途中の座標を増やし、直線を描画する回数を増やす必要がある事がわかります。

綺麗な曲線を描くというのは、直線を何度も描くという結構な処理となります。

■曲線の上を移動する

キャラクターを曲線の通りに移動させる事ができます。

0.0 から 1.0 まで少しずつ値を増やしながら座標を取得する事により、曲線の上を少しずつ移動される事ができます。

現在の座標の「曲線の進行方向（角度）」が知りたい場合は、「現在の座標」から「0.001 ほど加算した値の座標」までのベクトルから計算します。

上に戻る

２次ベジェ曲線を描画する

サンプルをダウンロード

curve_00_fla06_as1.fla Macromedia Flash MX ActionScript1.0

■２次ベジェ曲線の特徴

２次ベジェ曲線は、

開始座標、制御座標、終了座標の 3 点を指定する曲線です。

開始座標と終了座標は必ず通過します。

Adobe Flash のベジェツールで絵を描くときは３次ベジェ曲線ですが、 swf ファイルに書き出した時点ですべて２次ベジェ曲線に変換されます。

２次ベジェ曲線のほうが計算処理が少なく効率よく描画できます。

■２次ベジェ曲線用の関数

２次ベジェ曲線用の関数を見てみましょう。

■２次ベジェ曲線上の１つの座標を取得する

開始座標から終了座標までを 0 ～ 1 としてその間の点を取得する関数です。

第01引数に開始座標をオブジェクト型で指定
第02引数に制御座標をオブジェクト型で指定
第03引数に終了座標をオブジェクト型で指定
第04引数に 0.0 ～ 1.0 までの係数

計算結果の座標がオブジェクト型で返ります。

２次ベジェ曲線上の１つの座標を取得する


function QuadraticBezPoint( p0,p1,p2,d){

	var o = {x:0,y:0};

	var v = (1-d) * (1-d);
	o.x += v * p0.x;
	o.y += v * p0.y;

	v = 2 * d * (1-d);
	o.x += v * p1.x;
	o.y += v * p1.y;

	v = d * d;
	o.x += v * p2.x;
	o.y += v * p2.y;

	return o;
}

QuadraticBezPoint() 関数の使用例です。

QuadraticBezPoint() 関数の使用例


var p0 = {x:  0, y: 50};
var p1 = {x: 50, y:  0};
var p2 = {x:100, y:150};

var pos = QuadraticBezPoint(p0,p1,p2,0.5);

trace("x:" + pos.x + " y:" + pos.y);

■２次ベジェ曲線上の座標をまとめて取得する

開始点から終了点までに取得したい座標数を指定してまとめて座標を取得する関数です。

第01引数に開始座標をオブジェクト型で指定
第02引数に制御座標をオブジェクト型で指定
第03引数に終了座標をオブジェクト型で指定
第04引数に補間数

戻り値に座標がオブジェクト型の配列で返ります。

２次ベジェ曲線上の座標をまとめて取得する


function QuadraticBezStream( p0,p1,p2,interpolate){
	var i;
	var d = 0;
	var out = new Array();
	var v;
	var plus = 1.0 / (interpolate - 1);
	for(i=0;i < interpolate;i++){
		var o = {x:0,y:0};

		v = (1-d) * (1-d);
		o.x += v * p0.x;
		o.y += v * p0.y;

		v = 2 * d * (1-d);
		o.x += v * p1.x;
		o.y += v * p1.y;

		v = d * d;
		o.x += v * p2.x;
		o.y += v * p2.y;

		out[i] = o;
		d += plus;
	}

	return out;
}

QuadraticBezStream() 関数の使用例です。

QuadraticBezStream() 関数の使用例


var INTERPOLATE = 50;

var p0 = {x:  0, y: 50};
var p1 = {x: 50, y:  0};
var p2 = {x:100, y:150};

// ２次ベジェ曲線上の点を配列にして抽出
var list = QuadraticBezStream(p0,p1,p2,INTERPOLATE);

// 0-1, 1-2, 2-3,…の順番に線を引く
_root.clear();
_root.lineStyle(2, 0x000000, 100);
var i = 0;
for(i = 0;i < INTERPOLATE - 1; i++){
	_root.moveTo(list[i].x, list[i].y);
	_root.lineTo(list[i+1].x, list[i+1].y);
}

■２次ベジェ曲線上の１つの座標を取得する(３Ｄ座標)

開始座標から終了座標までを 0 ～ 1 としてその間の点を取得する関数です。

第01引数に開始座標をオブジェクト型で指定
第02引数に制御座標をオブジェクト型で指定
第03引数に終了座標をオブジェクト型で指定
第04引数に 0.0 ～ 1.0 までの係数

計算結果の座標がオブジェクト型で返ります。

２次ベジェ曲線上の１つの３Ｄ座標を取得する


function QuadraticBezPoint3D( p0,p1,p2,d){

	var o = {x:0,y:0,z:0};

	var v = (1-d) * (1-d);
	o.x += v * p0.x;
	o.y += v * p0.y;
	o.z += v * p0.z;

	v = 2 * d * (1-d);
	o.x += v * p1.x;
	o.y += v * p1.y;
	o.z += v * p1.z;

	v = d * d;
	o.x += v * p2.x;
	o.y += v * p2.y;
	o.z += v * p2.z;

	return o;
}

QuadraticBezPoint3D() 関数の使用例です。

QuadraticBezPoint3D() 関数の使用例


var p0 = {x:  0, y: 50,z:-100};
var p1 = {x: 50, y:  0,z:   0};
var p2 = {x:100, y:150,z: 100};

var pos = QuadraticBezPoint3D(p0,p1,p2,0.5);

trace("x:" + pos.x + " y:" + pos.y + " z:" + pos.z);

上に戻る

３次ベジェ曲線を描画する

サンプルをダウンロード

curve_01_fla06_as1.fla Macromedia Flash MX ActionScript1.0

■３次ベジェ曲線の特徴

３次ベジェ曲線は、開始座標、制御座標１、制御座標２、終了座標の４点を指定する曲線です。

開始座標と終了座標は必ず通ります。

曲線を動かすのに融通が利くため、図形ツールでよく使われます。

■３次ベジェ曲線用の関数

３次ベジェ曲線用の関数を見てみましょう。

■３次ベジェ曲線上の１つの座標を取得する

開始座標から終了座標までを 0 ～ 1 としてその間の点を取得する関数です。

第01引数に開始座標をオブジェクト型で指定
第02引数に制御座標１をオブジェクト型で指定
第03引数に制御座標２をオブジェクト型で指定
第04引数に終了座標をオブジェクト型で指定
第05引数に 0.0 ～ 1.0 までの係数

計算結果の座標がオブジェクト型で返ります。

３次ベジェ曲線上の１つの座標を取得する


function CubicBezPoint( p0,p1,p2,p3,d){

	var o = {x:0,y:0};

	var v = (1-d) * (1-d) * (1-d);
	o.x += v * p0.x;  
	o.y += v * p0.y;

	v = 3 * d * (1-d) * (1-d);
	o.x += v * p1.x;
	o.y += v * p1.y;

	v = 3 * d * d * (1-d);
	o.x += v * p2.x;
	o.y += v * p2.y;

	v = d * d * d;
	o.x += v * p3.x;
	o.y += v * p3.y;

	return o;
}

CubicBezPoint() 関数の使用例です。

CubicBezPoint() 関数の使用例


var p0 = {x:  0, y: 50};
var p1 = {x: 50, y:  0};
var p2 = {x:100, y:150};
var p3 = {x:150, y:100};

var pos = CubicBezPoint(p0,p1,p2,p3,0.5);

trace("x:" + pos.x + " y:" + pos.y);

■３次ベジェ曲線上の座標をまとめて取得する

開始点から終了点までに取得したい座標数を指定してまとめて座標を取得する関数です。

第01引数に開始座標をオブジェクト型で指定
第02引数に制御座標１をオブジェクト型で指定
第03引数に制御座標２をオブジェクト型で指定
第04引数に終了座標をオブジェクト型で指定
第05引数に補間数

戻り値に座標がオブジェクト型の配列で返ります。

３次ベジェ曲線上の座標をまとめて取得する


function CubicBezStream( p0,p1,p2,p3,interpolate){
	var i;
	var d = 0;
	var out = new Array();
	var v;
	var plus = 1.0 / (interpolate - 1);
	for(i=0;i < interpolate;i++){
		var o = {x:0,y:0};

		v = (1-d) * (1-d) * (1-d);
		o.x += v * p0.x;
		o.y += v * p0.y;

		v = 3 * d * (1-d) * (1-d);
		o.x += v * p1.x;
		o.y += v * p1.y;

		v = 3 * d * d * (1-d);
		o.x += v * p2.x;
		o.y += v * p2.y;

		v = d * d * d;
		o.x += v * p3.x;  
		o.y += v * p3.y;

		out[i] = o;
		d += plus;
	}

	return out;
}

CubicBezStream() 関数の使用例です。

CubicBezStream() 関数の使用例


var INTERPOLATE = 50;

var p0 = {x:  0, y: 50};
var p1 = {x: 50, y:  0};
var p2 = {x:100, y:150};
var p3 = {x:150, y:100};

// ３次ベジェ曲線上の点を配列にして抽出
var list = CubicBezStream(p0,p1,p2,p3,INTERPOLATE);

// 0-1, 1-2, 2-3,…の順番に線を引く
_root.clear();
_root.lineStyle(2, 0x000000, 100);
var i = 0;
for(i = 0;i < INTERPOLATE - 1; i++){
	_root.moveTo(list[i].x, list[i].y);
	_root.lineTo(list[i+1].x, list[i+1].y);
}

■３次ベジェ曲線上の１つの座標を取得する(３Ｄ座標)

開始座標から終了座標までを 0 ～ 1 としてその間の点を取得する関数です。

第01引数に開始座標をオブジェクト型で指定
第02引数に制御座標をオブジェクト型で指定
第03引数に終了座標をオブジェクト型で指定
第04引数に 0.0 ～ 1.0 までの係数

計算結果の座標がオブジェクト型で返ります。

３次ベジェ曲線上の１つの３Ｄ座標を取得する


function CubicBezPoint3D( p0,p1,p2,p3,d){

	var o = {x:0,y:0,z:0};

	var v = (1-d) * (1-d) * (1-d);
	o.x += v * p0.x;
	o.y += v * p0.y;
	o.z += v * p0.z;

	v = 3 * d * (1-d) * (1-d);
	o.x += v * p1.x;
	o.y += v * p1.y;
	o.z += v * p1.z;

	v = 3 * d * d * (1-d);
	o.x += v * p2.x;
	o.y += v * p2.y;
	o.z += v * p2.z;

	v = d * d * d;
	o.x += v * p3.x;
	o.y += v * p3.y;
	o.z += v * p3.z;

	return o;
}

CubicBezPoint3D() 関数の使用例です。

CubicBezPoint3D() 関数の使用例


var p0 = {x:  0, y: 50, z:-100};
var p1 = {x: 50, y:  0, z: -50};
var p2 = {x:100, y:150, z:  50};
var p3 = {x:150, y:100, z: 100};

var pos = CubicBezPoint3D(p0,p1,p2,p3,0.5);

trace("x:" + pos.x + " y:" + pos.y + " z:" + pos.z);

上に戻る

Ｎ次ベジェ曲線を描画する

サンプルをダウンロード

curve_02_fla06_as1.fla Macromedia Flash MX ActionScript1.0

■Ｎ次ベジェ曲線の特徴

制御座標を好きなだけ指定する曲線です。

開始座標と終了座標は必ず通ります。

計算量が多いので、ゲームに使う場合はこちらより、２次ベジェ曲線や３次ベジェ曲線の連続したデータを使用したほうがいいでしょう。

階乗を使って計算するので、変数に「整数型」を使用すると、数十個の頂点数で桁あふれを起こすので注意してください。

■Ｎ次ベジェ曲線用の関数

Ｎ次ベジェ曲線用の関数を見てみましょう。

■Ｎ次ベジェ曲線上の１つの座標を取得する

開始座標から終了座標までを 0 ～ 1 としてその間の点を取得する関数です。

第01引数に座標をオブジェクト型で複数格納した配列データを指定
第02引数に 0.0 ～ 1.0 までの係数

計算結果の座標がオブジェクト型で返ります。

Ｎ次ベジェ曲線上の１つの座標を取得する


function BezierPoint( list, d){
	var o = {x:0,y:0};
	var num = list.length;
	for(var i=0;i < num;i++){
		var p = list[i];
		var v = 1.0;
		var a = num - 1;    var b = i;    var c = a - b;
		for(;;){
			if(a > 1){ v *= a; a -= 1; } else { break; }
			if(b > 1){ v /= b; b -= 1; }
			if(c > 1){ v /= c; c -= 1; }
		}
		v *= Math.pow(d,i) * Math.pow(1-d,(num-1)-i);
		o.x += v * p.x;
		o.y += v * p.y;
	}
	return o;
}

BezierPoint() 関数の使用例です。

BezierPoint() 関数の使用例


var list = [
	{x:  0, y: 50},
	{x: 50, y:  0},
	{x:100, y:150},
	{x:150, y: 50},
	{x:200, y:  0}
];


var pos = BezierPoint(list,0.5);

trace("x:" + pos.x + " y:" + pos.y);

■Ｎ次ベジェ曲線上の座標をまとめて取得する

開始点から終了点までに取得したい座標数を指定してまとめて座標を取得する関数です。

第01引数に座標をオブジェクト型で複数格納した配列データを指定
第02引数に補間数

戻り値に座標がオブジェクト型の配列で返ります。

Ｎ次ベジェ曲線上の座標をまとめて取得する


function BezierStream( list, interpolate){
	var i,j;
	var d = 0;
	var out = new Array();
	var num = list.length;

	var plus = 1.0 / (interpolate - 1);

	for(j=0;j < interpolate;j++){
		var o = {x:0,y:0};
		for(i=0;i < num;i++){
			var p = list[i];
			var v = 1.0;
			var a = num - 1;    var b = i;    var c = a - b;

			for(;;){
					if(a > 1){ v *= a; a -= 1; } else { break; }
					if(b > 1){ v /= b; b -= 1; }
					if(c > 1){ v /= c; c -= 1; }
			}
			v *= Math.pow(d,i) * Math.pow(1-d,(num-1)-i);
			o.x += v * p.x;
			o.y += v * p.y;
		}

		out[j] = o;
		d += plus;
	}

	return out;
}

BezierStream() 関数の使用例です。

BezierStream() 関数の使用例


var INTERPOLATE = 50;

var pos = [
	{x:  0, y: 50},
	{x: 50, y:  0},
	{x:100, y:150},
	{x:150, y: 50},
	{x:200, y:  0}
];


// ベジェ曲線上の点を配列にして抽出
var list = BezierStream(pos,INTERPOLATE);

// 0-1, 1-2, 2-3,…の順番に線を引く
_root.clear();
_root.lineStyle(2, 0x000000, 100);
var i = 0;
for(i = 0;i < INTERPOLATE - 1; i++){
	_root.moveTo(list[i].x, list[i].y);
	_root.lineTo(list[i+1].x, list[i+1].y);
}

上に戻る

スプライン曲線を描画する

サンプルをダウンロード

curve_03_fla06_as1.fla Macromedia Flash MX ActionScript1.0

■スプライン曲線の特徴

制御座標を好きなだけ指定する曲線です。

すべての制御点を必ず通ります。

■スプライン曲線用の関数

スプライン曲線用の関数を見てみましょう。

■スプライン曲線上の座標をまとめて取得する

開始点から終了点までに取得したい座標数を指定してまとめて座標を取得する関数です。

第01引数に座標をオブジェクト型で複数格納した配列データを指定
第02引数に補間数

戻り値に座標がオブジェクト型の配列で返ります。

Ｎ次ベジェ曲線上の座標をまとめて取得する


function SplineStream (p, interpolate) {
	var num = p.length;
	var l = new Array();
	var _A = new Array();
	var _B = new Array();
	var _C = new Array();

	for (i=0; i < num-1; i++) {
		var p0 = p[i];
		var p1 = p[i+1];
		l[i] = Math.sqrt((p0.x - p1.x) * (p0.x - p1.x) + (p0.y - p1.y) * (p0.y - p1.y));
	}

	_A[0] = [0, 1, 0.5];
	_B[0] = {
		x:(3 / (2 * l[0])) * (p[1].x - p[0].x),
		y:(3 / (2 * l[0])) * (p[1].y - p[0].y)
	};
	_A[num-1] = [1, 2, 0];
	_B[num-1] = {
		x:(3 / l[num - 2]) * (p[num - 1].x - p[num - 2].x),
		y:(3 / l[num - 2]) * (p[num - 1].y - p[num - 2].y)
	};

	for (i=1; i < num-1; i++) {
		var a = l[i-1];
		var b = l[i];
		_A[i] = [b, 2.0 * (b + a), a];
		_B[i] = {
			x:(3.0 * (a * a * (p[i + 1].x - p[i].x)) + 3.0 * b * b * (p[i].x - p[i - 1].x)) / (b * a),
			y:(3.0 * (a * a * (p[i + 1].y - p[i].y)) + 3.0 * b * b * (p[i].y - p[i - 1].y)) / (b * a)
		};
	}
	for (i=1; i < num; i++) {
		var d = _A[i-1][1] / _A[i][0];

		_A[i] = [0, _A[i][1]*d-_A[i-1][2], _A[i][2]*d];
		_B[i].x = _B[i].x * d - _B[i - 1].x;
		_B[i].y = _B[i].y * d - _B[i - 1].y;

		_A[i][2] /= _A[i][1];
		_B[i].x /= _A[i][1];
		_B[i].y /= _A[i][1];
		_A[i][1] = 1;
	}

	_C[num-1] = {x:_B[num-1].x, y:_B[num-1].y};
	for (j=num-1; j > 0; j--) {
		_C[j-1] = {
			x:_B[j - 1].x-_A[j - 1][2] * _C[j].x,
			y:_B[j - 1].y-_A[j - 1][2] * _C[j].y
		};
	}

	var out = new Array();
	count = 0;
	for (i=0; i < num-1; i++) {
		var a = l[i];
		var _00 = p[i].x;
		var _01 = _C[i].x;
		var _02 = (p[i + 1].x - p[i].x) * 3 / (a * a) - (_C[i + 1].x + 2 * _C[i].x) / a;
		var _03 = (p[i + 1].x - p[i].x) * (-2/(a * a * a)) + (_C[i + 1].x + _C[i].x) * (1 / (a * a));
		var _10 = p[i].y;
		var _11 = _C[i].y;
		var _12 = (p[i + 1].y - p[i].y) * 3 / (a * a) - (_C[i + 1].y + 2 * _C[i].y) / a;
		var _13 = (p[i + 1].y - p[i].y) * (-2/(a * a * a)) + (_C[i + 1].y + _C[i].y) * (1 / (a * a));

		var t = 0;
		for (j=0; j < interpolate; j++) {
			out[count] = {
				x:((_03 * t + _02) * t + _01) * t + _00,
				y:((_13 * t + _12) * t + _11) * t + _10
			};
			count++;
			t += a / interpolate;
		}
	}
	out[count] = {
		x:p[num-1].x,
		y:p[num-1].y
	};

	return out;
}

SplineStream() 関数の使用例です。

SplineStream() 関数の使用例


var INTERPOLATE = 20;

var pos = [
	{x:  0, y: 50},
	{x: 50, y:  0},
	{x:100, y:150},
	{x:150, y: 50},
	{x:200, y:  0}
];

// スプライン曲線上の点を配列にして抽出
var list = SplineStream(pos,INTERPOLATE);

// 0-1, 1-2, 2-3,…の順番に線を引く
_root.clear();
_root.lineStyle(2, 0x000000, 100);
var i = 0;
for(i = 0;i < list.length - 1; i++){
	_root.moveTo(list[i].x, list[i].y);
	_root.lineTo(list[i+1].x, list[i+1].y);
}

上に戻る

前のページに戻る