Flashゲーム講座 & アクションスクリプトサンプル集


ランダムな数（乱数）を取得する



・乱数とは？
・乱数を取得する（小数値）
・乱数を取得する（整数値）
・擬似乱数を使用する
・連続しない乱数を取得する

前のページに戻る



乱数とは？

　


■乱数とは？

　
乱数は、決まった範囲内の中から適当に選び出した値です。
　
乱数を取得するたびに、サイコロを振るように予測できない適当な値が得られます。
　

上に戻る



乱数を取得する（0.0～0.999…）

　

サンプルをダウンロード
random_00_fla05_as1.flaMacroMedia Flash 5
　


■乱数を取得する

　
乱数を取得するには、Math.random() メソッドを使用します。
　
0.0 から 0.9999… までの小数値を取得することができます。(1.0 を含まない)
　
例) 0.0から0.999…までの小数を取得する

var r;
r = Math.random();
trace(r);
　
「 0.0 から 1.0 まで（1.0 は含まない）の小数値」にさらに好きな値を乗算すると、乱数を好きな範囲まで広げる事ができます。
　
例)約(0 ～ 100) までの乱数を取得 (100 ちょうどは取得できない)

var r;
r = Math.random() * 100;
trace(r);
　

■ -1 ～ 0.99999…までの値を取得する

　
まず、小数値の乱数を取得します。ここからさらに「 2 を掛けてから -1 」すると「 -1 から 0.9999… まで」の値となります。
　
乱数 (0.0 ～ 0.99999…) に 2 を掛けると(0.0 ～ 1.99999…) となります。
　
1 を減算すると (-1 ～ 0.99999…) となります。
　
例)-1 から 0.99999…まで取得する

var r;
r = Math.random() * 2 - 1;
trace(r);
　
「-1.0 から 1.0 までの（1.0 は含まない）小数値」にさらに好きな値を乗算すると、乱数を好きな範囲まで広げる事ができます。
　
例)約(-100 ～ 100) までの乱数を取得 (100 ちょうどは取得できない)

var r;
r = Math.random() * 2 - 1;
r = r * 100;
trace(r);
　

上に戻る



乱数を取得する（整数）

　

サンプルをダウンロード
random_01_fla05_as1.flaMacroMedia Flash 5
　


■整数値を取得する

　
Math.random()メソッドは、小数値しか取得できないので、計算して整数値に変換する必要があります。
　

■ 0 から数段階の整数値を取得する

　
まず、乱数を取得します。
　
得られた「0.0 から 1.0 までの（1.0 は含まない）小数値」に好きな整数値を乗算してから、Math.floor() メソッドを使って小数値を切り落とします。
　
例えば 10 段階の整数値が欲しいとします。
乱数 (0.0 ～ 0.99999…) に 10 を掛けると(0.0 ～ 9.99999…) となります。
小数部分を切り落とすと (0 ～ 9) となります。
　
例) 0,1,2 のどれかの値を取得する( 3 段階)

var r;
r = Math.floor(Math.random() * 3);
trace(r);
　
例) 0,1,2,3,4,5,6,7,8,9 のどれかの値を取得する( 10 段階)

var r;
r = Math.floor(Math.random() * 10);
trace(r);
　
ランダムで何段階かの処理の分岐をさせたい場合に便利です。
　
例) ランダムで 3 段階に処理を分ける

// 0 ～ 2 までの 3 段階の整数を取得
rand = Math.floor(Math.random() * 3);

if(rand == 0){

	/* 処理 1 */

}else if(rand == 1){

	/* 処理 2 */

}else if(rand == 2){

	/* 処理 3 */

}
　

■ x から数段階の整数値を取得する

　
まず、乱数を取得します。
　
得られた「0.0 から 1.0 までの（1.0 は含まない）小数値」に好きな整数値を乗算してから、Math.floor() メソッドを使って小数値を切り落とします。
　
最後に x を加算します。
　
例えば 8 から 5 段階の整数値が欲しいとします。
乱数 (0.0 ～ 0.99999…) に 5 を掛けると(0.0 ～ 4.99999…) となります。
小数部分を切り落とすと (0 ～ 4) となります。 8 を加算すると(8 ～ 12) となります。
　
例) 4,5,6 のどれかの値を取得する( 3 段階)

var r;
r = Math.floor(Math.random() * 3) + 3;
trace(r);
　
例) 13,14,15,16,17,18,19 のどれかの値を取得する( 7 段階)

var r;
r = Math.floor(Math.random() * 7 ) + 13;
trace(r);
　
計算用にランダムな値が欲しいときに便利です。
　
例) 10 ～ 30 のダメージを与える

// 体力
var life = 100;

// ランダムで10 ～ 30 のダメージ
var life -= Math.floor(Math.random() * 21) + 10;
　

上に戻る



擬似乱数を使用する

　


■擬似乱数とは？

　
パソコンは、ハードウェア的にランダムな数値を弾き出してくれるイメージがありますが実際はできません。
　
パソコンは、決められた計算しかできないので、次に算出される値はすべて確定しています。
　
「確定している数字の列」を使って、「あたかもランダムな値を算出しているように見せかける」事を擬似乱数といいます。
　
まず、何らかの値を返す「計算式」を用意します。
　
「計算式」は繰り返し実行すると、できるだけ前回とは違った数値が出現するようなアルゴリズムにします。
　
生成される数値は、取得したい範囲内の一部分にかたよらずに、均等に分散した値となるのが理想です。
　
数字の順序は確定しているが、その値は均等に分散している
　
　
「計算式」にいくら優れたアルゴリズムを用意しても、常に 0 回目から値を取得していてはランダムではありません。
　
そこで何らかの数値を使って、値の取得を開始する位置を変更します。
　
ちょっとだけ変更したくらいでは、簡単に推測される恐れがあります。開始位置は、天文学的に大きい数値でダイナミックにずらします。
　
開始位置をダイナミックにずらす事でランダムとみせかける
　
　
この開始位置をずらす為に使用する値を「乱数の種」といいます。
　
通常は、現在の時間を利用します。時間は常に変化しているので乱数の種として最適です。
　
時間を利用できないゲームボーイなどのハードウェアの場合、電源を入れてゲームを開始してから、決まった歩数で同じ敵とエンカウントする、決まった動作でスロットが大当たりするなど、同じ動作を再現できる方法が発見されて裏技になってたりしますね。
　
乱数をセーブしておいて次回起動時に乱数の種として使用したり、毎サイクル乱数を読み捨てたりすると、ユーザーが意図的に再現するのが難しくなります。
　
擬似乱数の品質を上げるためには、周期性も気にする必要があります。
　
「計算式」を繰り返し実行し続けると、いずれ「以前に出現した数値パターン」が生成されるようになります。これを「周期性」と言います。
　
「計算式」のアルゴリズムは、周期性が天文学的に長くなるのが理想です。
　

■有名な擬似乱数のアルゴリズム

　
有名な擬似乱数のアルゴリズムとして、メルセンヌツイスターがあります。
　
●Mersenne Twister Home Page
http://www.math.sci.hiroshima-u.ac.jp/~m-mat/MT/mt.html
　




■ メルセンヌツイスターを使用する

　
上記サイトで公開されているメルセンヌツイスターのソースの一部を AS1.0 関数で記述したのが下のソースになります。
　
メルセンヌツイスターのソースの一部をAS1.0関数で記述した例

var MT_N = 624;
var MT_M = 397;

var MATRIX_A	= 0x9908b0df;
var UPPER_MASK	= 0x80000000;
var LOWER_MASK	= 0x7fffffff;


// ------------------------------------------------------------------------------------------------
//	初期化
// ------------------------------------------------------------------------------------------------
function MersenneTwisterInitialize(seed){
	var a,b,al,ah,bl,bh,cl,ch;

 	var mti = MT_N + 1;
	var mt = new Array();

	mt[0] = seed & 0xffffffff;
	for (mti = 1; mti < MT_N ; mti++) {
	
		a  = 1812433253;
		b  = mt[mti-1] ^ (mt[mti-1] >>> 30);
		al = a & 0xFFFF;
		ah = a >>> 16;
		bl = b & 0xFFFF;
		bh = b >>> 16;
		cl = (al * bl) + mti;
		ch = (cl >>> 16) + ((al * bh) & 0xFFFF)  + ((ah * bl) & 0xFFFF);

		mt[mti] = ((ch << 16) | (cl & 0xFFFF)); 
		mt[mti] &= 0xffffffff;
	}

	return {
		mti : mti,
		mt : mt
	};
}


// ------------------------------------------------------------------------------------------------
//	-2147483648 ～ 2147483647 までの乱数を取得
// ------------------------------------------------------------------------------------------------
function MersenneTwisterGetInt32(obj){
    var y;
    var mag01 = [0x0, MATRIX_A];

    if (obj.mti >= MT_N) {
        var kk;

        if (obj.mti == MT_N+1)	 obj = MersenneTwisterInitialize(5489);

        for (kk = 0 ; kk < MT_N - MT_M ; kk++) {
            y = (obj.mt[kk] & UPPER_MASK) | (obj.mt[kk+1] & LOWER_MASK);
            obj.mt[kk] = obj.mt[kk+MT_M] ^ (y >>> 1) ^ mag01[y & 0x1];
        }
        for (;kk < MT_N-1;kk++) {
            y = (obj.mt[kk] & UPPER_MASK) | (obj.mt[kk+1] & LOWER_MASK);
            obj.mt[kk] = obj.mt[kk+(MT_M-MT_N)] ^ (y >>> 1) ^ mag01[y & 0x1];
        }
        y = (obj.mt[MT_N-1] & UPPER_MASK) | (obj.mt[0] & LOWER_MASK);
        obj.mt[MT_N-1] = obj.mt[MT_M-1] ^ (y >>> 1) ^ mag01[y & 0x1];

        obj.mti = 0;
    }
  
    y = obj.mt[obj.mti++];

    y ^= (y >>> 11);
    y ^= (y <<  7) & 0x9d2c5680;
    y ^= (y << 15) & 0xefc60000;
    y ^= (y >>> 18);

    return y;
}


// ------------------------------------------------------------------------------------------------
//	0 ～ 0.999999…までの乱数を取得
// ------------------------------------------------------------------------------------------------
function MersenneTwisterGetFloat(obj){
	var r = MersenneTwisterGetInt32(obj)*(1.0/4294967296.0); 
	if(r < 0)	r += 1.0;
	return r;
}
　

■ 上記関数の使い方

　
上記のメルセンヌツイスターソースの使い方です。
　
■初期化する（乱数の種をセットする）
　
まず、MersenneTwisterInitialize() 関数を呼び出して初期化します。
　
引数に「乱数の種」として整数値を指定します。戻り値にオブジェクトが返ります。
　
例) 乱数の種をセットして初期化する

// 乱数の種
var seed = 0;

// 初期化
var mt_obj = MersenneTwisterInitialize(seed);
　
■符号付き整数値を取得する
　
MersenneTwisterGetInt32() 関数を呼び出すと、乱数（整数値）を取得する事ができます。
　
引数に、初期化時に生成したオブジェクトを渡します。戻り値に -2147483648 ～ 2147483647 までの整数値が返ります。 何度も呼び出す事が可能です。
　
例) -2147483648 ～ 2147483647 までの整数値を取得

// 乱数の種
var seed = 0;

// 初期化
var mt_obj = MersenneTwisterInitialize(seed);

// 乱数を生成
var value1 = MersenneTwisterGetInt32(mt_obj);
var value2 = MersenneTwisterGetInt32(mt_obj);
var value3 = MersenneTwisterGetInt32(mt_obj);
　
■小数値を取得する
　
MersenneTwisterGetFloat() 関数を呼び出すと、乱数（小数値）を取得する事ができます。
　
引数に、初期化時に生成したオブジェクトを渡します。戻り値に 0.0 ～ 0.99999… までの小数値が返ります。 何度も呼び出す事が可能です。
　
例) 0.0 ～ 0.99999… までの小数値を取得

// 乱数の種
var seed = 0;

// 初期化
var mt_obj = MersenneTwisterInitialize(seed);

// 乱数を生成
var value1 = MersenneTwisterGetFloat(mt_obj);
var value2 = MersenneTwisterGetFloat(mt_obj);
var value3 = MersenneTwisterGetFloat(mt_obj);
　

■乱数の種を固定して使用する例

　
ユニークな乱数の種をセットする事ができればランダムとなりますが、ゲームでは、あえて同じ乱数の種をセットして使うことがあります。
　
例えば、タイムアタックなどのモードでは、公平さを出すためにゲーム開始直前に決まった乱数の種をセットしてランダム要素を排除します。
　
また、プレイヤーが操作したゲーム状況を再び再現する「リプレイ機能」を実装したいとします。プレイヤーが押したキー情報をすべて保存しておいて リプレイ開始時に同じ操作を再現する事で実現できます。しかし、乱数を使用していると毎回実行するたびに変化してしまい同一の処理の再現できません。
そこでゲーム開始時とリプレイ開始時に、同じ値で乱数の種を初期化する事でまったく同じプログラム処理を再現する事ができます。
　

上に戻る



連続しない乱数を取得する

　


■乱数をそのまま使うと…？

　
サイコロを連続で振ってみると下のような、Ａというパターンと、Ｂというパターンになったとします。
　
パターンＡ
　
パターンＡは乱数で得られた結果をそのまま表示しています。たまに同じ値が連続して出現している事が確認できます。
　
パターンＢ
　
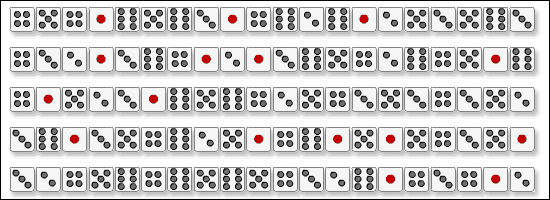
パターンＢは乱数で得られた結果にさらに前回と同じ値にならないように手を加えています。
　
パターンＡの方が同じ目が連続して出現するのを見て、「乱数の品質が悪いのではないか？」と誤解される方がいます。
　
サイコロを振ってどんな目が出るかは常に 1/6 の確率で決まるので、低確率ですが同じ値が出現する事はありえます。
　
同じ値が絶対に連続して出現しないようにしたいのであれば、乱数で得られた値をそのまま使うのではなく意図した動作になるよう加工する必要があります。
　

■低確率でかたよる問題

　
乱数をそのまま使うと低確率ですが、近い値が連続して出現するという事があります。 この問題は低確率で発生する事だから…と許容してしまうと、結果的に品質を下げてしまう事になります。
　
例えば、花火のようなパーティクルエフェクトを作りたいとします。 発生源から扇状に粒子を飛び散らせたいので初速の部分に乱数をそのまま使ったとします。
　
粒子の数が少なすぎると結構な頻度で粒子がかたよります。綺麗に分散しないので、粒子の数を増やす事で対応してしまいがちです。 しかし、粒子増やすだけでは、見た目が悪くなる確率が下がったにすぎません。100 人が閲覧すれば 1 人は見栄えの悪いパーティクルに遭遇するかもしれません。
　
またゲームの場合、パーティクルは贅沢なエフェクトです。少ない枚数で見栄えよく作れるのであれば少なく抑えます。
　
乱数をそのまま使用せずに、意図した動作となるよう加工してから利用すれば、確実に見た目が綺麗な事を保障しつつ、粒子の数も少なく抑える事ができるかもしれません。
　

■前回得られた乱数が出現したら破棄してもう一度取得してみる

　
乱数を取得したときに、得られた結果を変数に残しておきます。
　
次に乱数を取得するときに、得られた結果が退避した変数と一致する場合もう一度乱数を取得します。 一致しなければ取得成功とし、得られた結果を変数に残しておきます。
　
これを繰り返します。
　
例) 前回得られた乱数が出現したら破棄してもう一度取得する

// --------------------------------------------
// 連続しない乱数を取得するための処理
// --------------------------------------------
var rand_old = 0;
function RandGetInt(range){

	// エラー
	if(range <= 1){
		return 0;
	}
	
	while(true){
		// 乱数を取得
		var r = Math.floor(Math.random() * range);
		
		// 前回と一致しなければ終了
		if(r != rand_old){
			break;
		}
	}
	
	// 結果を退避
	rand_old = r;
	
	return r;
}


// --------------------------------------------
// 乱数を 30 個取得して表示
// --------------------------------------------
var i;
for(i=0;i < 30;i++){
	var r = RandGetInt(5);
	trace(r);
}
　

■シャッフルしてみる

　
あらかじめ取得したい番号を配列に格納して、中身をシャッフルしておきます。
　
乱数を取得したいときに配列の先頭から順番に取り出します。
　
これを繰り返します。
　
例) シャッフルを行う

var i;

// シャッフルしたい数値を配列に格納
var rand_array = new Array();
for(i=0;i < 30;i++){
	rand_array[i] = i;
}

// 配列をシャッフルする
var num = rand_array.length;	// 配列の数
for(i=0;i < num;i++){
	// ランダムな番地を取得
	var r = Math.floor(Math.random() * num);

	// i とランダムな番地の中身を入れ替え
	var t = rand_array[r];
	rand_array[r] = rand_array[i];
	rand_array[i] = t;
}


// 配列を先頭から取り出す
for(i=0;i < num;i++){
	var r = rand_array.shift();
	trace(r);
}
　

上に戻る


前のページに戻る