プロジェクション変換とは?
■プロジェクション変換とは?
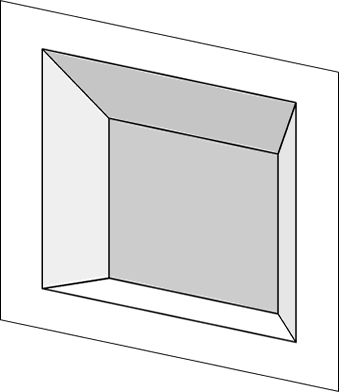
3Dゲームを見ているとあたかも3D空間が広がっているように見えますが、実際は2Dであるモニタ上に表示されています。
3D座標をあたかも3D空間のようにみえるパースのきいた2D座標へ変換する手法をプロジェクション変換といいます。
変換したい3D座標を準備する
■変換したい3D座標を準備する
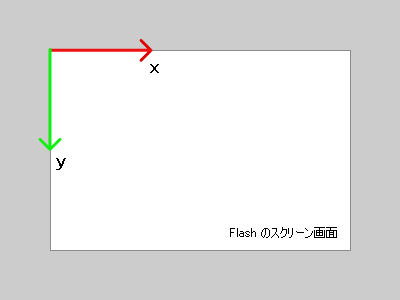
Flash の画面は右に x 軸、下に y 軸が伸びる2次元座標です。
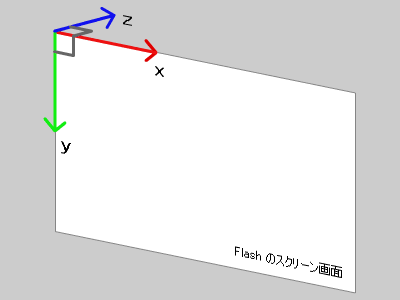
この2次元座標上の奥方向に z 軸を追加して3次元空間としてみます。
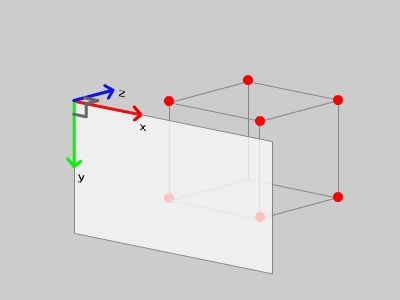
変換したい3次元の座標をオブジェクト型で用意してみます。
変換したい3D座標を列挙する
var d3_pos = {
{x : 100, y : 50, z : 100},
{x : 300, y : 50, z : 100},
{x : 300, y : 250, z : 100},
{x : 100, y : 250, z : 100},
{x : 100, y : 50, z : 300},
{x : 300, y : 50, z : 300},
{x : 300, y : 250, z : 300},
{x : 100, y : 250, z : 300}
};
大体、下の図のような配置となります。
平行投影変換を使う
■平行投影変換の考え方
3次元空間に座標を配置した状態です。

この状態で、すべての3D座標の z 座標を 0 にしてみるとどうなるでしょう?
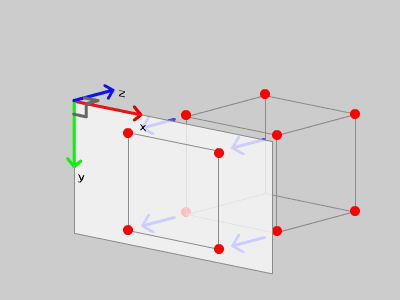
すべての座標がFlashスクリーン上に集まりました。
この変換を平行投影変換といいます。
奥行きが感じられませんが3Dから2Dへの変換の表現の1つとなります。
■平行投影変換式
平行投影変換の式です。 z 座標を取っただけです。
平行投影変換式
スクリーン上の x 座標 = 3次元の x 座標;
スクリーン上の y 座標 = 3次元の y 座標;
■実際に変換してみる
3D上の座標を2D上の座標に平行投影変換し、Flash 上で表示する例です。
平行投影変換式の公式
// 3次元座標
var d3_pos = [
{x : 100, y : 50, z : 100},
{x : 300, y : 50, z : 100},
{x : 300, y : 250, z : 100},
{x : 100, y : 250, z : 100},
{x : 100, y : 50, z : 300},
{x : 300, y : 50, z : 300},
{x : 300, y : 250, z : 300},
{x : 100, y : 250, z : 300}
];
// 2次元座標を格納するバッファ
var i;
var num = d3_pos.length;
var d2_pos = new Array();
for (i=0; i < num; i++) {
d2_pos[i] = new Object();
}
// 平行投影変換
for (i=0; i < num; i++) {
d2_pos[i].x = d3_pos[i].x;
d2_pos[i].y = d3_pos[i].y;
}
// Flash上に表示
var shape = new Shape();
var g = shape.graphics;
stage.addChild (shape);
g.lineStyle (0, 0xFFAAAA, 1.0);
for (i=0; i < num; i++) {
g.drawCircle ( d2_pos[i].x, d2_pos[i].y , 5);
}
透視投影変換を使う
■透視投影変換(パースペクティブプロジェクション)の考え方
3D座標から奥行き間のあるパースのきいた2D座標への変換を行うには、透視投影変換を使います。
下の図のように3D空間上に柱を並べてみました。
下の図のように3D空間上に柱を並べてみました。
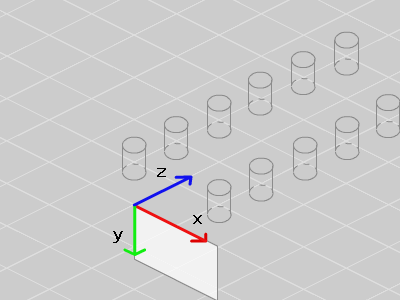
この状態で、 x 座標と y 座標をそれぞれ z 座標で割るとどうなるでしょう?
スクリーン (z = 0) から遠ざかるほど z 座標は大きくなります。
大きい値で割るほど 0 に近づくので x 座標と y 座標は下のような曲線上に変換されます。
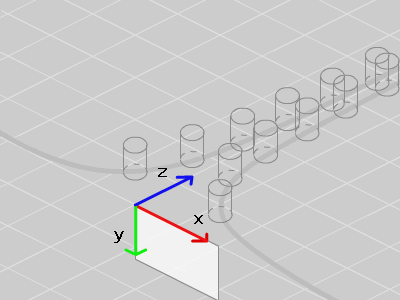
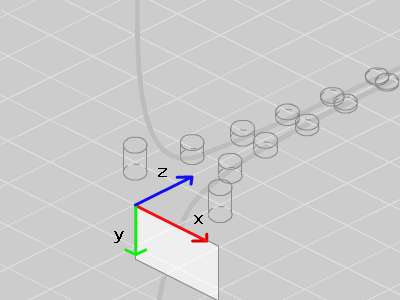
この状態で すべての z 座標を 0 にしてスクリーン上に集めてみます。
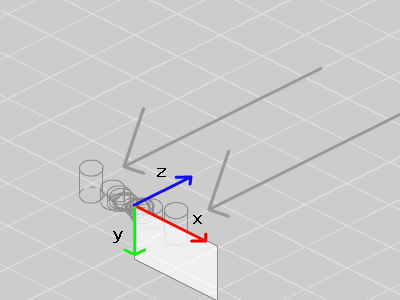
スクリーン座標系の原点を中心にパースがかかった2次元の座標に変換できました。
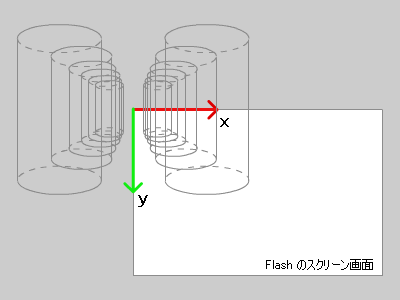
2次元座標系の原点を中心にパースがかかっているという事は、
3Dの空間に視点(カメラ)があるとしたら、原点に配置されz方向を向いていると考える事ができます。
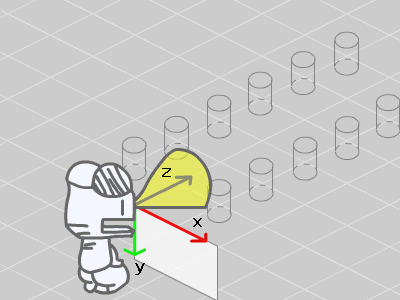
このままでは、Flash のスクリーン上の原点である画面左上を中心にパースがかかっている絵になってしまいます。
通常は、画面中央を中心にパースをかけたいので、全体を中央に移動させます。
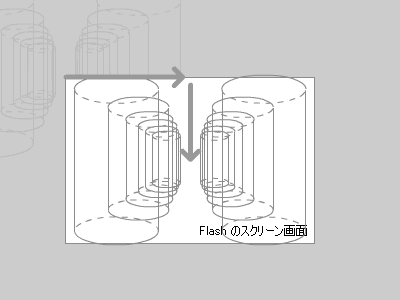
ここまで紹介したのはあくまでイメージ図で、実際に z 座標で割るだけだとパースがきつ過ぎて立体に見えません。
さらに透視投影変換に必要となるパラメータを見てみましょう。
■透視投影変換に必要なパラメータ
透視投影変換を行うためには 視野角 と 画面解像度 という2つのパラメータが必要となります。
■視野角について
視野角の違いは、下のFlashで確認できます。
視野角が広いほど奥行き感が増加します。
また、ズームアウトする感じになり周りの映る範囲が広がります。カメラを回転させるとパースがきき過ぎて歪んでいる感じがします。
逆に視野角が狭いほど奥行き感が減少します。
ズームインする感じになり周りの映る範囲が狭くなります。カメラ回転時の違和感が少なくなります。
45 ~ 60度くらいが3Dゲームでもよく使われているようです。
■画面解像度について
もうひとつの 画面解像度 は、3Dの変換結果をスクリーン上に表示するときのサイズになります。
例えば Flash の画面が 幅:400 高さ:300 で、この大きさにぴったり合うように描画したい場合は、幅:400 高さ:300 という数値が画面解像度となります。
例えば Flash の画面が 幅:400 高さ:300 で、この大きさにぴったり合うように描画したい場合は、幅:400 高さ:300 という数値が画面解像度となります。
■透視投影変換式
透視投影変換の式です。すべての座標をこの式を通して変換します。
視野角には好きな角度を指定する事ができます。
透視投影変換の式
var angle = 1 ~ 180 の好きな数値; // 視野角
var fov = 1 / Math.tan(angle * 0.5 * Math.PI / 180); // 視点からの距離
var width = 解像度の『幅』か『高さ』のどちらか大きい方の数値 * 0.5;
var height = width * 倍率; // アスペクト比(通常は 1.0)
スクリーン上の x 座標 = 3次元の x 座標 / 3次元の z 座標 * fov * width;
スクリーン上の y 座標 = 3次元の y 座標 / 3次元の z 座標 * fov * height;
『3Dの座標系の y 軸が上』で、『2D座標系の y 軸が下』だったといった座標系の向きの違いがある場合は、この段階でマイナスを掛けてつじつまを合わせます。
■実際に変換してみる
透視投影変換の式を参考にして3D座標から2D座標に変換してみましょう。
3D座標をすべて透視投影変換する
// 3次元座標
var d3_pos = [
{x : 100, y : 50, z : 1000},
{x : 300, y : 50, z : 1000},
{x : 300, y : 250, z : 1000},
{x : 100, y : 250, z : 1000},
{x : 100, y : 50, z : 3000},
{x : 300, y : 50, z : 3000},
{x : 300, y : 250, z : 3000},
{x : 100, y : 250, z : 3000}
];
// 2次元座標を格納するバッファ
var i;
var num = d3_pos.length;
var d2_pos = new Array();
for (i=0; i < num; i++) {
d2_pos[i] = new Object();
}
var angle = 60; // 視野角
var w = 400; // 解像度幅
var h = 300; // 解像度高さ
var size = ((w > h) ? w : h) * 0.5;
var fov = 1 / Math.tan(angle * 0.5 * Math.PI / 180)
for (i=0; i < num; i++) {
// 平行投影変換
d2_pos[i].x = d3_pos[i].x / d3_pos[i].z * fov * size;
d2_pos[i].y = d3_pos[i].y / d3_pos[i].z * fov * size;
// 左上の原点を中心としたパースがかかるので画面の中心にパースがかかるように中央へ移動
d2_pos[i].x += w / 2;
d2_pos[i].y += h / 2;
}
// Flash上に表示
var shape = new Shape();
var g = shape.graphics;
stage.addChild (shape);
g.lineStyle (0, 0xFFAAAA, 1.0);
for (i=0; i < num; i++) {
g.drawCircle ( d2_pos[i].x, d2_pos[i].y , 10 / d3_pos[i].z * fov * size);
}
2D系の座標になると z 座標は不要になる気がしますが、この数値は奥行きを表しているので、描画順を決める上でとても重要なパラメータとなります。
ここでは数値が高いほど奥になります。
ここでは数値が高いほど奥になります。
なお z 座標がマイナスの値になる座標は、カメラの反対側になるので描画対象から外します。