円同士の衝突を計算する
サンプルをダウンロード
サンプルをダウンロード
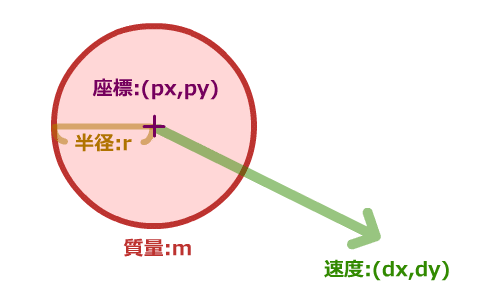
■衝突する円を表現するのに必要なパラメータ
円の衝突に必要なパラメータは以下の通りです。
円の中心座標を、変数 (px, py) とします。
円の速度を、変数 (dx, dy) とします。
円の半径を、変数 r とします。
円の質量を、変数 m とします。お好みで設定します。
円の速度を、変数 (dx, dy) とします。
円の半径を、変数 r とします。
円の質量を、変数 m とします。お好みで設定します。
 |
円の衝突に必要なパラメータ
// 円A
var ca = {
px : 0, // x 座標
py : 0, // y 座標
dx : 2, // x 方向の速度
dy : 3, // y 方向の速度
r :10, // 半径
m : 1 // 質量
};
// 円B
var ca = {
px : 0, // x 座標
py : 0, // y 座標
dx : 2, // x 方向の速度
dy : 3, // y 方向の速度
r :10, // 半径
m : 1 // 質量
};
■円同士が衝突したか調べる(簡易チェック)
円同士で当たり判定があるかを調べます。
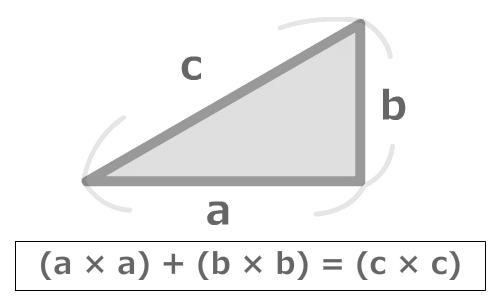
三平方の定理から…
 |
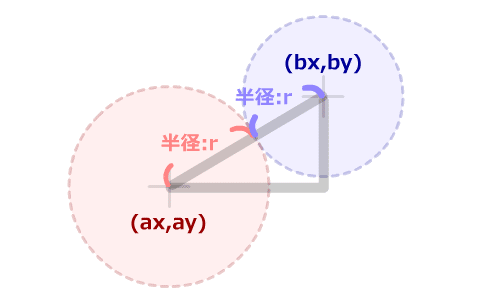
「円Aの中心座標」から「円Bのの中心座標」までの距離が、「円Aの半径」と「円Bの半径」を足した値より小さければ、めり込んでいる事がわかります。
 |
円Aと円Bが重なっているか調べる
if((b.px - a.px) * (b.px - a.px) + (b.py - a.py) * (b.py - a.py) < (a.r + b.r) * (a.r + b.r)){
// 当たりあり
}
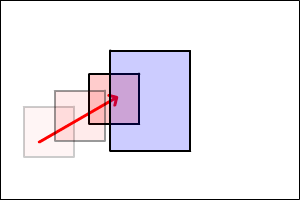
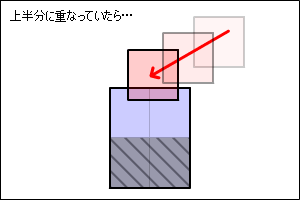
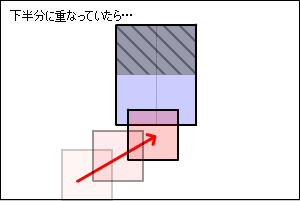
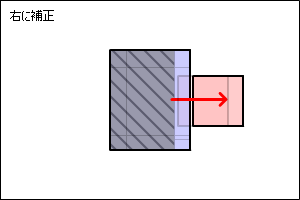
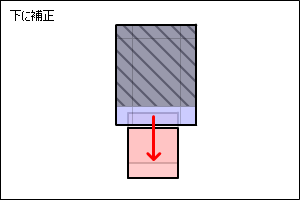
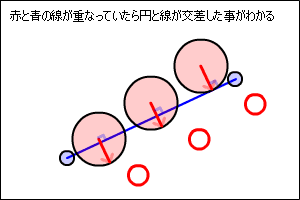
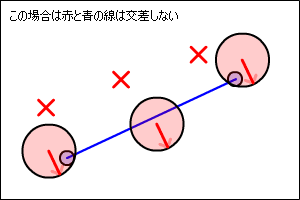
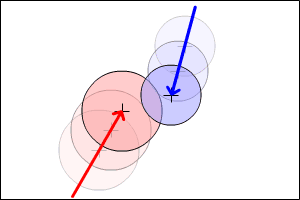
当たっている事がわかれば、めり込まない位置まで座標を移動する必要があります。
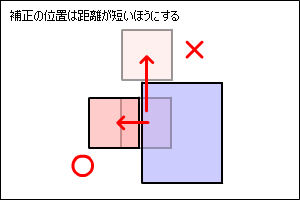
このとき下の図のように、
時間をさかのぼるように進行方向を逆に戻る補正が理想ですが、計算が複雑です。

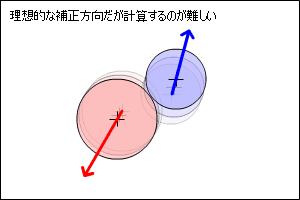
ここでは、簡単に計算ができる方法で妥協してみます。
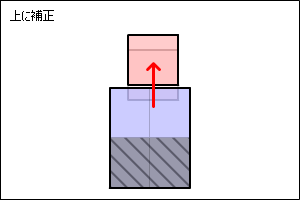
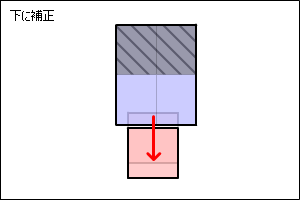
以下の図のように最短の距離で離すようにしてみます。

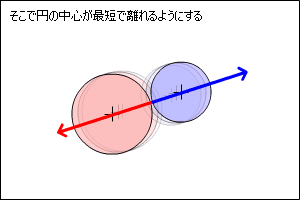
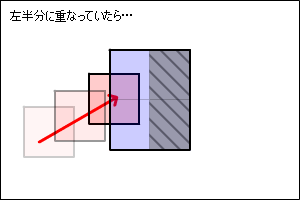
まずめり込んだ量を調べます。
円Bから円Aまでのベクトルを調べて距離を取得します。
円Aと円Bの半径を足して、距離を引けば、めり込んだ長さが得られます。
円Aと円Bのめり込んだ量を調べる
var vx = (a.px - b.px);
var vy = (a.py - b.py);
var len = Math.sqrt(vx * vx + vy * vy);
var distance = (a.r + b.r) - len;
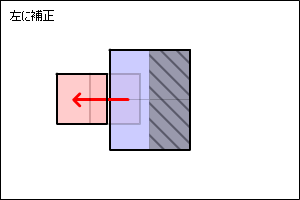
円Aの補正方向を調べます。
円Bから円Aまでのベクトルを正規化します。
円Bの補正方向は、このベクトルを反転したものになります。
円Aの補正方向を調べる
var vx = (a.px - b.px);
var vy = (a.py - b.py);
var len = Math.sqrt(vx * vx + vy * vy);
var distance = a.r + b.r - len;
if(len > 0) len = 1 / len;
vx *= len;
vy *= len;
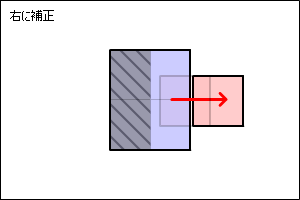
めり込んだ長さの半分ずつを補正方向に移動します。
円Aと円Bを重ならない位置まで補正する
var vx = (a.px - b.px);
var vy = (a.py - b.py);
var len = Math.sqrt(vx * vx + vy * vy);
var distance = a.r + b.r - len;
if(len > 0) len = 1 / len;
vx *= len;
vy *= len;
distance /= 2.0;
a.px += vx * distance;
a.py += vy * distance;
b.px -= vx * distance;
b.py -= vy * distance;
これで、円同士が重なっているかの判定と、円同士を重ならない位置まで補正する事ができました。
次は、より詳細な衝突判定の検出を調べてみましょう。
■円同士がいつ衝突するか調べる(精密チェック)
円Aと円Bが、いずれ衝突するとします。
衝突までに必要なフレーム時間を f とします。
円同士が衝突した瞬間は、点で接触する事になります。このときの、
円Aの座標を (ax , ay) とします。
円Bの座標を (bx , by) とします。
これらのパラメータを求めてみたいと思います。
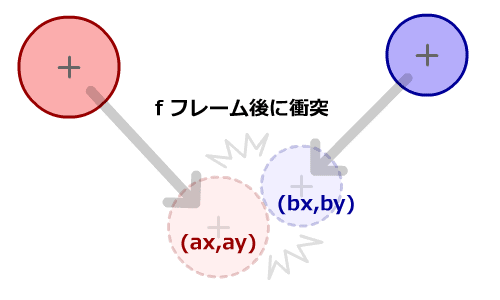 |
円Aの現在の位置から、 f フレーム時間移動し続けると、衝突する瞬間の座標に到達します。
円Aが f フレーム時間移動すると衝突した瞬間の座標(ax , ay)となる
ax = a.px + a.dx * f … (1)
ay = a.py + a.dy * f … (2)
円Bの現在の位置から、 f フレーム時間移動し続けると、衝突する瞬間の座標に到達します。
円Bが f フレーム時間移動すると衝突した瞬間の座標(bx , by)となる
bx = b.px + b.dx * f … (3)
by = b.py + b.dy * f … (4)
三平方の定理から…
 |
衝突した瞬間の「円Aの中心座標」から「円Bのの中心座標」までの距離は、「円Aの半径」と「円Bの半径」を足した値に等しくなります。
 |
三平方の定理から、中心座標の距離と、2つの円の半径を足した値が等しくなる
(ax - bx) * (ax - bx) + (ay - by) * (ay - by) = (a.r + b.r) * (a.r + b.r) … (5)
この5つの式から、フレーム時間 f を求める事ができます。
式を整理して二次方程式( ax2 + bx + c = 0 ) の形にまとめます。
三平方の定理から、中心座標の距離と、2つの円の半径を足した値が等しくなる
ax = a.px + a.dx * f
ay = a.py + a.dy * f
bx = b.px + b.dx * f
by = b.py + b.dy * f
(ax - bx) * (ax - bx) + (ay - by) * (ay - by) = (a.r + b.r) * (a.r + b.r)
↓
(ax * ax) - (ax * bx) -
(ax * bx) + (bx * bx) +
(ay * ay) - (ay * by) -
(ay * by) + (by * by) = (a.r + b.r) * (a.r + b.r)
↓
((a.px + a.dx * f) * (a.px + a.dx * f)) - ((a.px + a.dx * f) * (b.px + b.dx * f)) -
((a.px + a.dx * f) * (b.px + b.dx * f)) + ((b.px + b.dx * f) * (b.px + b.dx * f)) +
((a.py + a.dy * f) * (a.py + a.dy * f)) - ((a.py + a.dy * f) * (b.py + b.dy * f)) -
((a.py + a.dy * f) * (b.py + b.dy * f)) + ((b.py + b.dy * f) * (b.py + b.dy * f)) = (a.r + b.r) * (a.r + b.r)
↓
((a.px * a.px) + (a.px * a.dx * f) + (a.dx * f * a.px) + (a.dx * f * a.dx * f)) -
((a.px * b.px) + (a.px * b.dx * f) + (a.dx * f * b.px) + (a.dx * f * b.dx * f)) -
((a.px * b.px) + (a.px * b.dx * f) + (a.dx * f * b.px) + (a.dx * f * b.dx * f)) +
((b.px * b.px) + (b.px * b.dx * f) + (b.dx * f * b.px) + (b.dx * f * b.dx * f)) +
((a.py * a.py) + (a.py * a.dy * f) + (a.dy * f * a.py) + (a.dy * f * a.dy * f)) -
((a.py * b.py) + (a.py * b.dy * f) + (a.dy * f * b.py) + (a.dy * f * b.dy * f)) -
((a.py * b.py) + (a.py * b.dy * f) + (a.dy * f * b.py) + (a.dy * f * b.dy * f)) +
((b.py * b.py) + (b.py * b.dy * f) + (b.dy * f * b.py) + (b.dy * f * b.dy * f)) = (a.r + b.r) * (a.r + b.r)
( (a.px * a.px) + (a.px * a.dx * f) + (a.dx * a.px * f) + (a.dx * a.dx * f * f)) +
( - (a.px * b.px) - (a.px * b.dx * f) - (a.dx * b.px * f) - (a.dx * b.dx * f * f)) +
( - (a.px * b.px) - (a.px * b.dx * f) - (a.dx * b.px * f) - (a.dx * b.dx * f * f)) +
( (b.px * b.px) + (b.px * b.dx * f) + (b.dx * b.px * f) + (b.dx * b.dx * f * f)) +
( (a.py * a.py) + (a.py * a.dy * f) + (a.dy * a.py * f) + (a.dy * a.dy * f * f)) +
( - (a.py * b.py) - (a.py * b.dy * f) - (a.dy * b.py * f) - (a.dy * b.dy * f * f)) +
( - (a.py * b.py) - (a.py * b.dy * f) - (a.dy * b.py * f) - (a.dy * b.dy * f * f)) +
( (b.py * b.py) + (b.py * b.dy * f) + (b.dy * b.py * f) + (b.dy * b.dy * f * f)) = (a.r + b.r) * (a.r + b.r)
↓
(f * f) * ((a.dx * a.dx) - (a.dx * b.dx) - (a.dx * b.dx) + (b.dx * b.dx) + (a.dy * a.dy) - (a.dy * b.dy) - (a.dy * b.dy) + (b.dy * b.dy)) +
( f) * ((a.px * a.dx) + (a.dx * a.px) - (a.px * b.dx) - (a.dx * b.px) - (a.px * b.dx) - (a.dx * b.px) + (b.px * b.dx) + (b.dx * b.px) + (a.py * a.dy) + (a.dy * a.py) - (a.py * b.dy) - (a.dy * b.py) - (a.py * b.dy) - (a.dy * b.py) + (b.py * b.dy) + (b.dy * b.py)) +
((a.px * a.px) - (a.px * b.px) - (a.px * b.px) + (b.px * b.px) + (a.py * a.py) - (a.py * b.py) - (a.py * b.py) + (b.py * b.py) - (a.r + b.r) * (a.r + b.r)) = 0:
「二次方程式の根の公式」を使って解くと、答えは2つ得られます。
1つ目は、接触する瞬間のフレーム時間 f0 です。
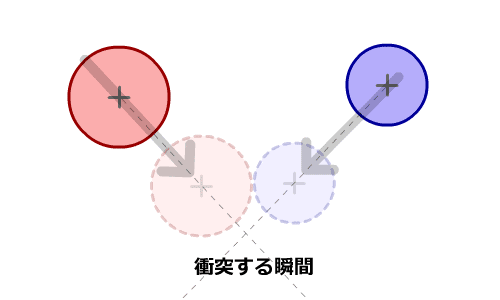 |
2つ目は、円同士が通り抜けて離れる瞬間のフレーム時間 f1 です。
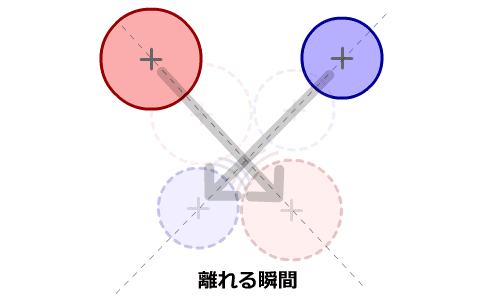 |
フレーム時間を計算する
var _a = (a.dx * a.dx) - 2 * (a.dx * b.dx) + (b.dx * b.dx) + (a.dy * a.dy) - 2 * (a.dy * b.dy) + (b.dy * b.dy);
var _b = 2 * (a.px * a.dx) - 2 * (a.px * b.dx) - 2 * (a.dx * b.px) + 2 * (b.px * b.dx) + 2 * (a.py * a.dy) - 2 * (a.py * b.dy) - 2 * (a.dy * b.py) + 2 * (b.py * b.dy);
var _c = (a.px * a.px) - 2 * (a.px * b.px) + (b.px * b.px) + (a.py * a.py) - 2 * (a.py * b.py) + (b.py * b.py) - (a.r + b.r) * (a.r + b.r);
var _d = Math.sqrt(_b * _b - 4 * _a * _c);
var f0 = (- _b - _d) / (2 * _a); // 接触する瞬間
var f1 = (- _b + _d) / (2 * _a); // 離れる瞬間
f0 と f1 の値から以下の事がわかります。
| 値 | 状態 |
| f0 と f1 がどちらもプラス | 円同士は近づいている |
| f0 と f1 どちらもマイナス | 円同士は離れている |
| f0 と f1 の符号が反転 | 円同士はめり込んでいる |
| f0 が 0 以上、 1 以下の値 | 現在のフレームで衝突する |
f0 から、衝突後の座標を計算します。
衝突する瞬間の座標を計算する
var ax = a.px + a.dx * f0;
var ay = a.py + a.dy * f0;
var bx = b.px + b.dx * f0;
var by = b.py + b.dy * f0;
円同士が衝突しない場合は、この式が成り立たないとき…?という事で、
平方根を計算する部分が 0 以下になる場合、円同士は衝突しないと判定してみます。
フレーム時間を計算する
var _a = (a.dx * a.dx) - 2 * (a.dx * b.dx) + (b.dx * b.dx) + (a.dy * a.dy) - 2 * (a.dy * b.dy) + (b.dy * b.dy);
var _b = 2 * (a.px * a.dx) - 2 * (a.px * b.dx) - 2 * (a.dx * b.px) + 2 * (b.px * b.dx) + 2 * (a.py * a.dy) - 2 * (a.py * b.dy) - 2 * (a.dy * b.py) + 2 * (b.py * b.dy);
var _c = (a.px * a.px) - 2 * (a.px * b.px) + (b.px * b.px) + (a.py * a.py) - 2 * (a.py * b.py) + (b.py * b.py) - (a.r + b.r) * (a.r + b.r);
var _d = _b * _b - 4 * _a * _c;
if(_d <= 0){
// 当たりなし
}else{
// 当たりあり
_d = Math.sqrt(_d);
var f0 = (- _b - _d) / (2 * _a); // 接触する瞬間
var f1 = (- _b + _d) / (2 * _a); // 離れる瞬間
}
これで円Aと円Bが衝突するかしないかの判定と、
衝突するまでのフレーム時間と、
点で接触してるときの円Aの座標と円Bの座標
が求まりました。
次は、衝突後の移動方向を調べてみましょう。
■円同士の衝突後の方向を調べる
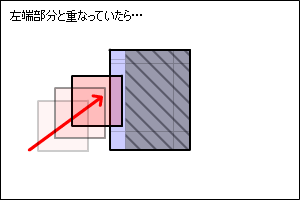
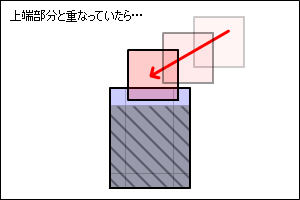
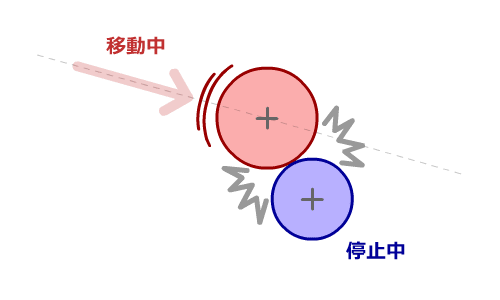
下の図のようにクリーンヒットした場合は、勢いのある反応がありそうです。
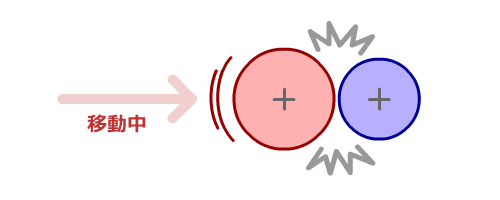 |
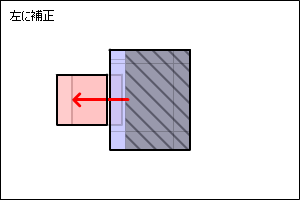
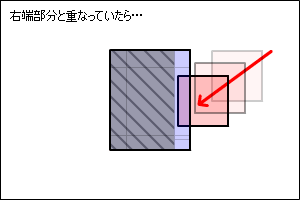
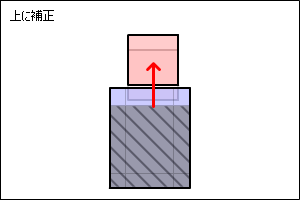
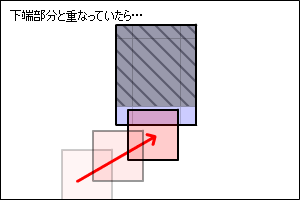
逆に、下の図のようにカスヒットした場合は、勢いが無さそうです。
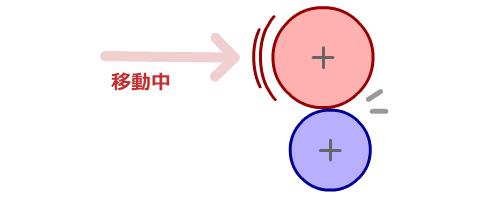 |
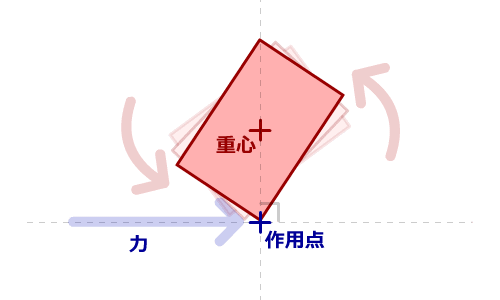
「力の方向」と、「作用点から重心までの方向」が同じ場合、
移動運動が発生し、回転運動は発生しません。
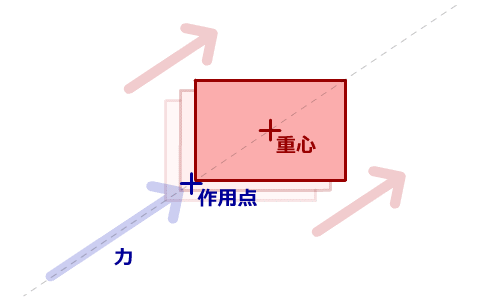 |
「力の方向」と、「作用点から重心までの方向」が 垂直である場合、
移動運動は発生しなくなり、回転運動が発生します。
 |
では円Aと円Bの速度ベクトルを、「移動運動を発生させるベクトル」と「回転運動を発生させるベクトル」の2つに分離してみます。
 |
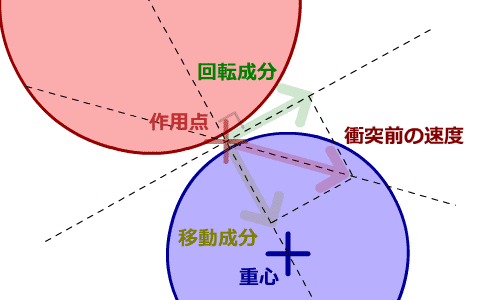 |
円Aから円Bへ移動運動を発生させるベクトルを(amx,amy) とします。
円Aから円Bへ回転運動を発生させるベクトルを(arx,ary) とします。
円Bから円Aへ移動運動を発生させるベクトルを(bmx,bmy) とします。
円Bから円Aへ回転運動を発生させるベクトルを(brx,bry) とします。
速度ベクトルを重心方向と垂直な方向に分離する
var t;
var vx = (b.px - a.px);
var vy = (b.py - a.py);
t = -(vx * a.dx + vy * a.dy) / (vx * vx + vy * vy);
var arx = a.dx + vx * t;
var ary = a.dy + vy * t;
t = -(-vy * a.dx + vx * a.dy) / (vy * vy + vx * vx);
var amx = a.dx - vy * t;
var amy = a.dy + vx * t;
t = -(vx * b.dx + vy * b.dy) / (vx * vx + vy * vy);
var brx = b.dx + vx * t;
var bry = b.dy + vy * t;
t = -(-vy * b.dx + vx * b.dy) / (vy * vy + vx * vx);
var bmx = b.dx - vy * t;
var bmy = b.dy + vx * t;
回転運動を発生させるベクトルですが、今回は回転を考慮しないのでそのままにします。
移動運動を発生させるベクトル同士を使って衝突を計算してみたいと思います。
衝突を計算するためには、反発係数 e が必要になります。
反発係数 e には 0.0 ~ 1.0 までのお好みの値を設定します。
反発係数を設定する
var e = 1.0; // 反発係数
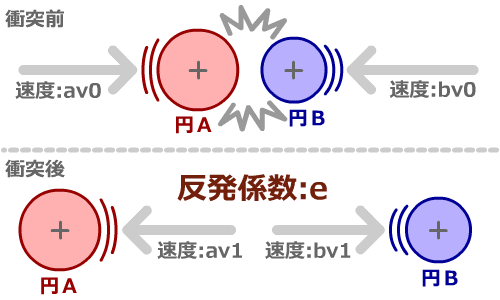
さて、円同士が正面衝突したとします。
円Aの衝突前の速度を av0 、衝突後の速度を av1
円Bの衝突前の速度を bv0 、衝突後の速度を bv1
円Aの質量を am
円Bの質量を bm
とします。
 |
まず反発係数は、以下の関係があります。
反発係数
e = - (bv1 - av1) / (bv0 - av0) … (1)
速度と質量を乗算すると、運動量となります。
運動量を計算する
運動量 = 質量 × 速度
運動量保存の法則により、衝突前の円の運動量の合計値と、衝突後の円の運動量の合計値は等しくなります。
運動量保存の法則
am * av0 + bm * bv0 = am * av1 + bm * bv1 … (2)
この2つの式を使うと衝突後の速度がわかります。
式を整理してみます。
2つの式を整理する
e = - (bv1 - av1) / (bv0 - av0)
am * av0 + bm * bv0 = am * av1 + bm * bv1
↓
bv1 = - e * (bv0 - av0) + av1
am * av0 + bm * bv0 = am * av1 + bm * bv1
↓
am * av0 + bm * bv0 = am * av1 + bm * (- bv0 * e + av0 * e + av1)
↓
am * av0 + bm * bv0 = am * av1 - bv0 * e * bm + av0 * e * bm + av1 * bm;
↓
am * av0 + bm * bv0 + bv0 * e * bm - av0 * e * bm = av1 * ( am + bm);
↓
av1 = (am * av0 + bm * bv0 + bv0 * e * bm - av0 * e * bm) / (am + bm)
bv1 = - e * (bv0 - av0) + av1
この式を使って、x 軸方向と y 軸方向でそれぞれ計算します。
これで移動運動を発生させるベクトル同士の、衝突後のベクトルが求まります。
x 方向と y 方向それぞれの衝突後の速度を計算する
var e = 1.0;
var adx = (a.m * amx + b.m * bmx + bmx * e * b.m - amx * e * b.m) / (a.m + b.m);
var bdx = - e * (bmx - amx) + adx;
var ady = (a.m * amy + b.m * bmy + bmy * e * b.m - amy * e * b.m) / (a.m + b.m);
var bdy = - e * (bmy - amy) + ady;
回転運動を発生させるベクトルを加算すると、衝突後の速度となります。
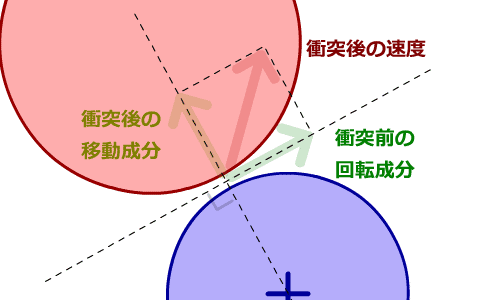 |
回転運動を発生させるベクトルを加算して衝突後の速度を計算
a.dx = adx + arx;
a.dy = ady + ary;
b.dx = bdx + brx;
b.dy = bdy + bry;
これで衝突後の速度が求まりました。
矩形を使った地形との衝突を計算する
サンプルをダウンロード
サンプルをダウンロード
矩形のパラメータ |
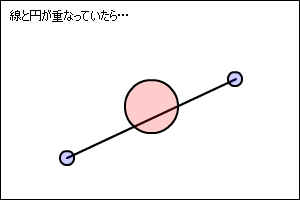
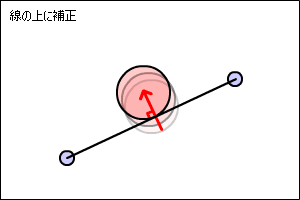
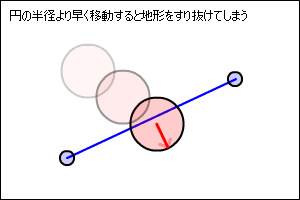
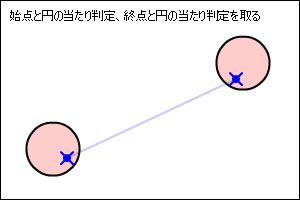
円と線を使った地形との衝突を計算する
サンプルをダウンロード
円と線のパラメータ |