交差判定について

レイとは？

レイとは弾丸を意味します。

弾丸を銃から発射して見ることにします。弾丸は、銃の座標から移動を開始します。弾丸は速度を持ってるので、どの方向にどの力で飛ぶかという値を持っています。

　

　

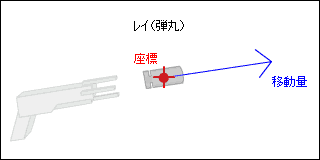
この座標と移動量を持つ物体をここではレイと呼びます。

という訳で、移動させたいMCを用意します。このムービークリップに座標と1フレームあたりの移動量という2つのパラメータを持たせましょう。

　

x = 0; // x 座標 y = 0; // y 座標 dx = 10; // x 移動量 dy = 10; // y 移動量

　

レイと線との交差判定とは？

レイと線との交差判定というのは、以下のようなあたりを調べることです。

　

　

線を表現してみよう

レイと当たり判定を求める線ですが、2点の座標で表現することにします。ここではまだ線分ではなく線なので長さは無限に伸びていると考えてください

　

ax = 80; // 座標A ax = 70; bx = 320; // 座標B bx = 150;

　

　

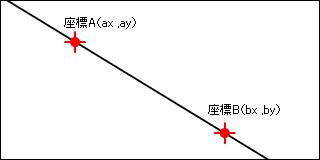
この線を線ABと呼ぶことにします。

　

線の法線

座標A から座標B に線を引いてから >時計回りに90度まわしてみましょう。左下方向に垂直な線ができると思います。

この線ABに対して垂直な線を法線と言います。

　

　

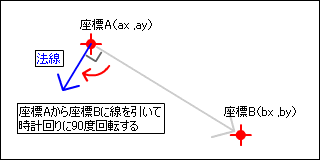
レイと線の交差判定

レイの移動ベクトルをどれくらい伸ばせば線と交差点に到達するか調べます。この倍率を t とします。

　

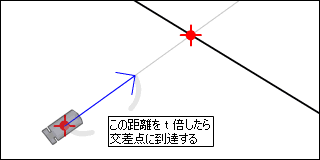
線の法線を調べます。座標ベクトル B から座標ベクトル A を引いてベクトルABを求めます。

var abx = bx - ax; var aby = by - ay;

　

時計回りに90度回転します。

var nx = -aby; var ny = abx;

　

法線を正規化します。

　

var length = Math.sqrt((nx * nx) + (ny * ny)); if(length > 0) length = 1 / length; nx *= length; ny *= length;

　

とりあえず下の式で t が求まります。

　

var d = -(ax * nx + ay * ny); var t = -(nx * x + ny * y + d) / (nx * dx + ny * dy);

　

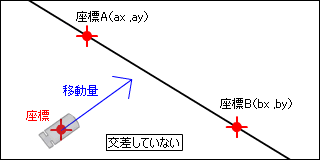
さて、t がマイナスの値のときはどういう状態でしょうか。下の図のように、レイが線にの方向ではなく反対向きになっています。



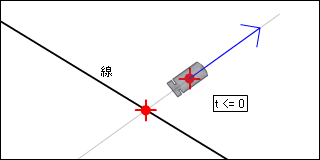
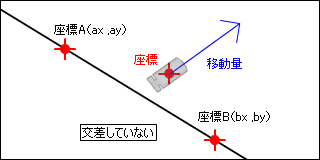
t が 1 より大きい場合はどうでしょうか？レイの移動量を伸ばせばいずれ線と交わりますが、交差はしていません。



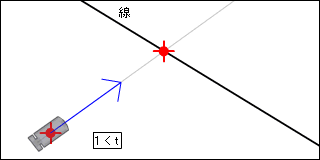
t が、0 の場合は移動量が 0 の時か線分に対して平行なので交差しません。

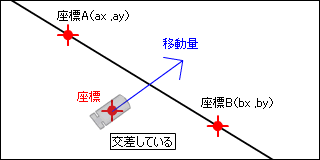
と言うことは t が 0 より大きく 1 以下の場合は交差していることがわかります。

　

　

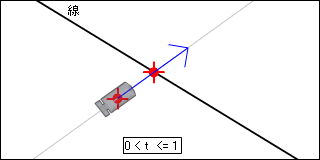
交差している座標を求めよう

移動量を t 倍すると交差するので、移動量ベクトルを t 倍してから、座標ベクトルを加算してみましょう。

　

cx = x + dx * t; cy = y + dy * t;

　

なお交点は、tが 0 の場合を除いて必ず求まるので、レイを線と置けば、線と線の交差座標を調べるのに使えます。

　

レイと線分とで当たり判定を取るには？

　

　

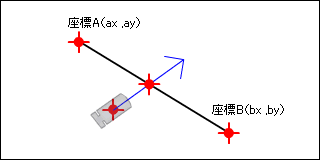
ここまで線で考えてきましたが、線分の当たり判定を取るためには、ここからさらに交差座標が線分の中に入っているのか調べる必要があります。そこで今度は内積を使います。

　

内積とは？

　

内積とは2つの単位ベクトルの平行の度合いを表しています。
単位ベクトル=長さが1のベクトル

　

特徴としては、
2つのベクトルが同じ向きで平行のときは 1 になります。
2つのベクトルが垂直のときは 0 になります。
2つのベクトルが逆向きで平行のときは -1 になります。
（注.２つのベクトルが正規化されてる場合）

　

内積は以下の式で求まります。
ベクトルA(ax ,ay)とベクトルA(bx ,by) の内積

　

var doc = (ax * bx) + (ay * by);

　

　

交差座標が線分の中に入っているか調べる

この内積を使ってどうやって線分の中に座標があるか調べるのかと言う話ですが、交差座標を座標Cとします。 ベクトルACと、ベクトルBCを作って内積を調べてみましょう。

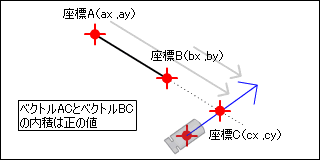
交差座標が左上に出た場合です。2つのベクトルは同じ向きに平行なので、この場合内積は正の値となります。

　

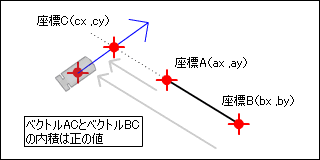
交差座標が右下に出た場合です。2つのベクトルは同じ向き平行なので、この場合も内積は正の値となります。

　

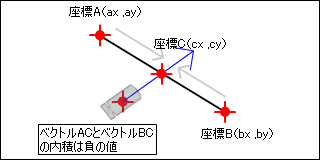
交差座標が線分の中に入っている場合です。2つのベクトルは逆向きに平行なので、この場合は内積が負の値となります。ということは、>内積の結果が負であれば、交差座標は、線分の中に入っていると言うことになります。

　

　

座標ベクトル C から座標ベクトル A を引いてベクトルACを求めます。

var acx = cx - ax; var acy = cy - ay;

座標ベクトル C から座標ベクトル B を引いてベクトルBCを求めます。

var bcx = cx - bx; var bcy = cy - by;

ベクトルAC とベクトル BC とで内積を求めます。

var doc = (acx * bcx) + (acy * bcy);

内積の結果が正の場合、交点は線分の外にあります。内積の結果が負の場合、交点は線分の中にあります。

if(doc < 0){ // 当たりあり }else{ // 当たりなし }

　

これでレイと線分との交差判定を取ることができます。レイは線分なので、この当たり判定を使えば線分と線分の交差判定が取れる事になります。

　

衝突について

円と線分を使った地形衝突の処理をこちらにまとめています。